设智力在全人口中的分布服从正态分布(3)

对数正态分布(logarithmic normal distribution):一个随机变量的对数服从正态分布,则该随机变量服从对数正态分布。

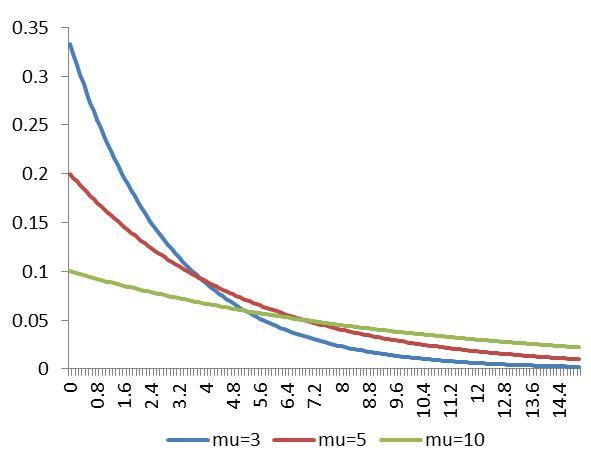
指数分布

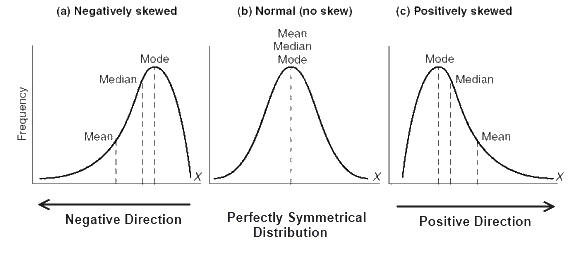
正如我们所看到的正偏态分布的曲线,众数 \u003C中位数 \u003C平均值。

概率密度函数:其中,gam(x)为伽马函数 14. 正态平方卡方分布 :服从正态分布的变量的平方服从卡方分布。

当样本服从尖峰肥尾分布的时候,偏度也为零,但和正态分布不同:中间部分更高,左右两个尾巴更厚,如图2所示: 当分布的高峰向右偏移,长尾向左延伸时,分布为左偏,偏度为负,如图3所示: 当分布的高峰向左偏移,长尾向右侧延伸时,分布为右偏,偏度为正,如图4

在本例中,如果取显著性水平α=0.01,通过查《标准正态分布表》,则临界值就会发生变化,拒绝域也会

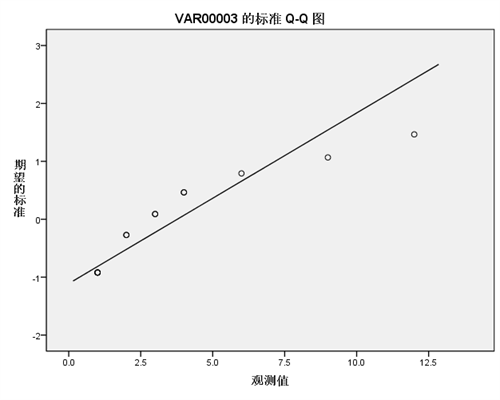
2)pp图和qq图: 是对比正态分布的累积概率值和实际分布的累积概率值。

五、抽样分布(sampling distributions) 1.中心极限定理(central limit theorem) 设从均值为μ,方差为σ2的任意一个总体中抽取样本量为n的样本,当n充分大时,样本均值的抽样分布近似服从均值为μ、方差为σ2

累积分布函数的反函数可以用来生成服从该随机分布的随机变数。

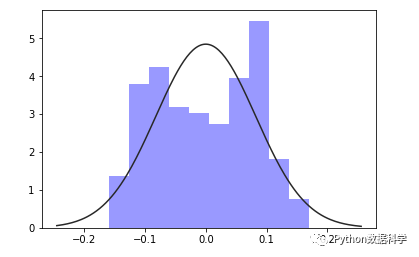
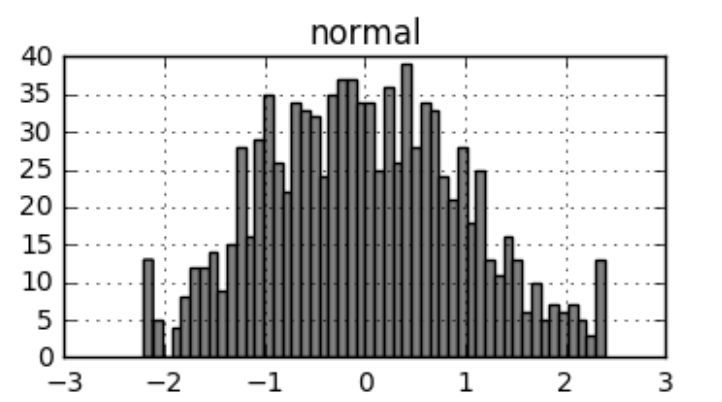
现生成一组服从正态分布的随机数,sample.hist表示产生直方图,更多绘图方法会在下一章节进行讲解: ▲图5-11:未处理噪声时的变量直方图 对p

控制图中异常值是指一组测定值中与平均值的偏差超过两倍标准差的测定值。

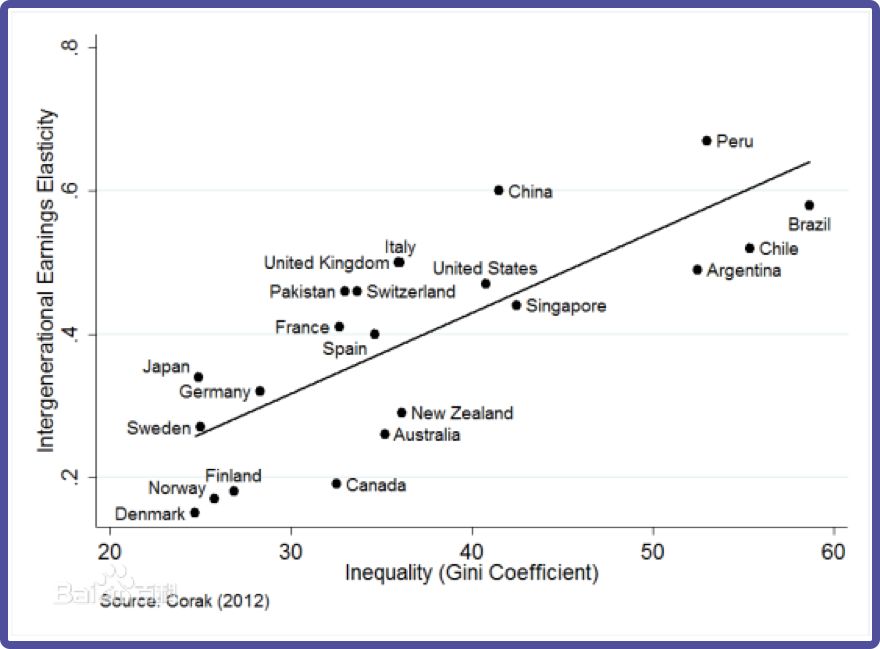
其中横轴是基尼系数,代表收入差距,纵轴为“代际收入弹性”,即父辈的收入水平对下一代收入水平的影响,该数值越大,表示收入的代际流动性越低,子女处于父辈的经济阶层的可能性就越高。

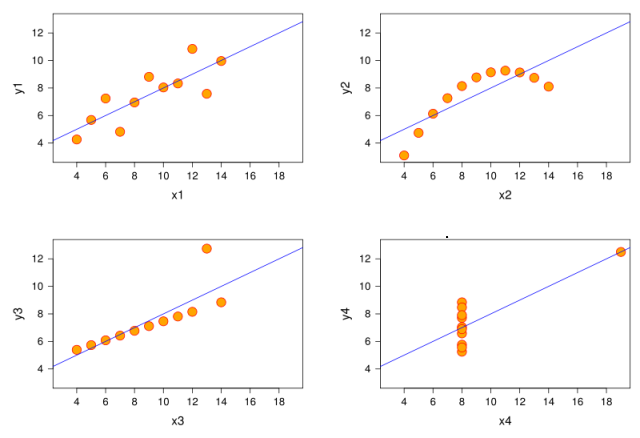
以上四个散点图对应的数据的皮尔逊相关系数均为0.816.